2021年埼玉県－４

解答

（１）解説参照

（２）$BE=3 cm$

（３）$\frac{6}{5} cm^2$

解説・解き方の例

図のように,$\angle BAC$の二等分線と辺$BC$との交点を$F$,線分$AF$と線分$EC$との交点を$G$とします。

（３）$\triangle ABC$の面積が$18 cm^2$であるとき、$\triangle GFC$の面積を求めなさい。

いくつか解き方があると思いますが、一つ紹介します。

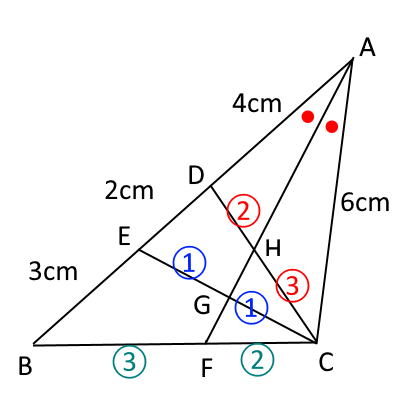
上の図を見てください($AF$と$CD$の交点を$H$としています）。 $AF$が$\angle BAC$の二等分線になっていることから、前にあげた二等分線の性質を使って、 例えば次のことがわかります。

1. $AD:AC=DH:HC$より、$DH:HC=4:6=2:3$
2. $AE:AC=EG:GC$より、$EG:GC=6:6=1:1$
3. $AB:AC=BF:FC$より、$BF:FC=9:6=3:2$

ここで、$\triangle EBC$と$\triangle GFC$に注目すると、 $FG:GC=1:1$、$BF:FC=3:2$より、面積比は辺の比を使って次のように計算できる。 $$\triangle EBC : \triangle GFC=CE\times CB:CG\times CF\\=2\times 5:1\times2=10:2=5:1$$ となる。よって、$\triangle GFC$は$\triangle EBC$の$\frac{1}{5}$である。

また、$AE:EB=6:3=2:1$であることから、$\triangle ABC:\triangle EBC=3:1$であるので、 $\triangle ABC=18 cm^2$より、$\triangle EBC=6 cm^2$である。

よって、 $$\triangle GFC = \triangle EBC \times \frac{1}{5}=6 \times \frac{1}{5}=\frac{6}{5} cm^2$$ となる

問題

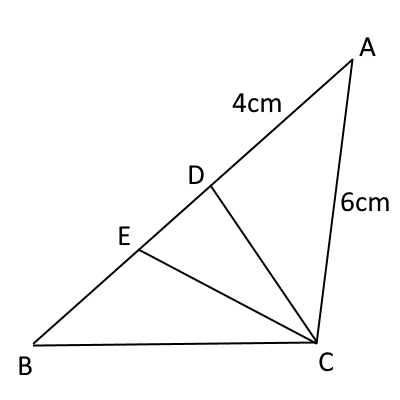
図のように$\triangle ABC$の辺$AB$上に、$\angle ABC= \angle ACD$となる点$D$をとります。

また、$\angle BCD$ の二等分線と辺$AB$との交点を$E$とします。$AD=4cm,AC=6cm$であるとき、次の各問いに答えなさい。

（１）$\triangle ABC$と$\triangle ACD$が相似であることを証明しなさい。

（２）$BE$の長さを求めなさい。

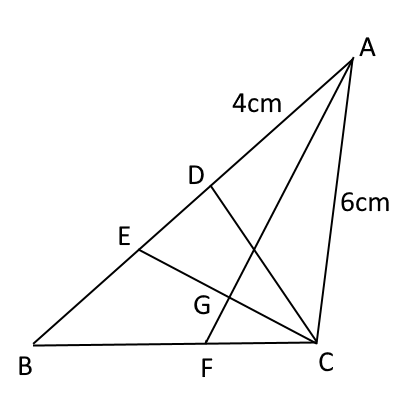
図のように,$\angle BAC$の二等分線と辺$BC$との交点を$F$,線分$AF$と線分$EC$との交点を$G$とします。

（３）$\triangle ABC$の面積が$18 cm^2$であるとき、$\triangle GFC$の面積を求めなさい。