2021年千葉県－４

解答

（１）解説参照

（２）$\sqrt{2} cm$

解説・解き方の例

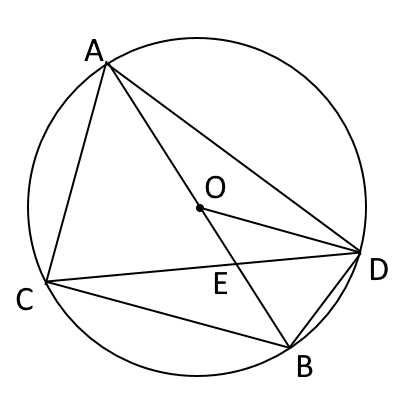
（１）

これは、問題に証明の一部が載っており、そこを穴埋めする形で答える問題になっています。

したがって、ここでは証明の要点だけを書きます。

• $\angle ADC = \angle ABC$（円周角）
• $\angle ABC=\angle BOD$（錯角）

より、$\angle ADC=\angle BOD$

$\angle ACD = \angle DBO$（円周角）

よって、$\triangle ACD ∽ \triangle DBO$ である（二角相等）。

（２）

次のような方針で解いてみます。

• やはり（１）で$\triangle ACD ∽ \triangle DBO$を証明しているのだから、これを使う。
• $\triangle DBO$の$BD$と対応するのは$\triangle ACD$の$AC$なので、$AC$の長さと、相似比がわかれば$BD$が求まるはずだ。

では、まずACを求めてみましょう。$AB$が直径なので、$\angle ACB=90°$ となるので、$\triangle ABC$が直角三角形になるので、三平方の定理から$AC$が求まりそうです。

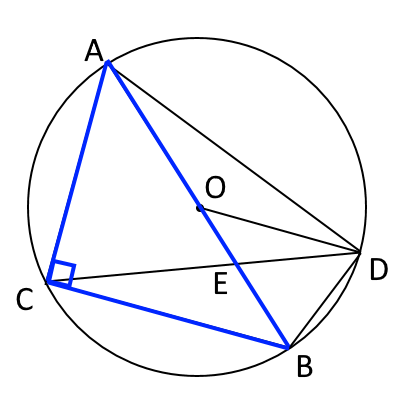
$AO=2 cm$より、円の半径が$2 cm$であり、$AB=4 cm$。$CB=3 cm$なので、$AC^2=AB^2-CB^2$ より $$AC=\sqrt{4^2-3^2}=\sqrt{7}$$ となります。

次に相似比を求めます。 $\triangle ACD$と$\triangle DBO$は相似です。ここで、$\triangle DBO$を見ると、$OB$と$OD$は半径なので、二等辺三角形であることがわかります。 したがって、$\triangle ADC$も二等辺三角形です。

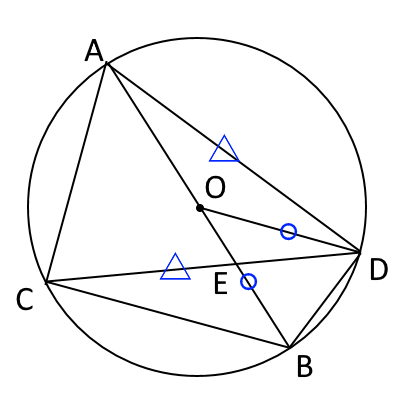
$\triangle OBC$の$OD=OB=2$というのはわかっているので、 $\triangle ADC$の$CD$の長さを求めれば相似比がわかります。 したがって、$CD$を求めるのが目標です。

ここで、半径$DO$を$AC$まで伸ばしてみます。次の図のように$OD$の延長線と$AC$の交点を$F$とします。

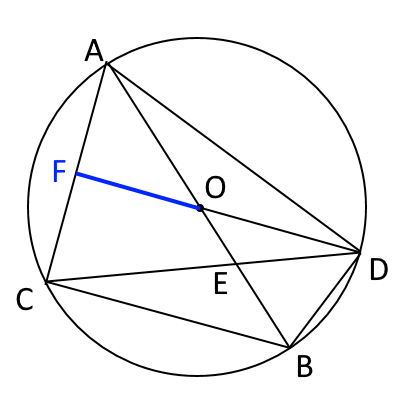
$OF$と$BC$は平行で、$AO=OB=半径$なので、中点連結定理から$$OF=\frac{1}{2}BC=\frac{1}{2}\times 3=\frac{3}{2}$$となります。

よって、$DF=DO+OF=2+\frac{3}{2}=\frac{7}{2}$となります。

ここで、$\triangle DFC$に着目します。

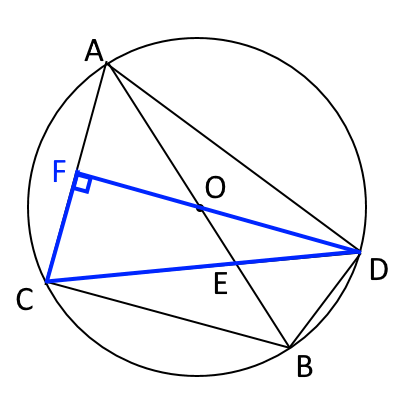
$\triangle DFC$は、$DF$が円の中心を通っているので、二等辺三角形の半分になり、 直角三角形になります。

$DF=\frac{7}{2}$、$CF=\frac{1}{2} \times \sqrt{7}=\frac{\sqrt{7}}{2}$より、 $$CD=\sqrt{CF^2+DF^2} =\sqrt{\left(\frac{\sqrt{7}}{2}\right)^2+\left(\frac{7}{2}\right)^2}=\sqrt{14}$$

よって、相似比は$CD:OB=\sqrt{14}:2$となる。

$AC=\sqrt{7}$なので、$AC:BD=CD:OB$より、 $$BD=AC\times \frac{2}{\sqrt{14}}=\sqrt{7}\times \frac{2}{\sqrt{14}}=\sqrt{2} cm$$ となる。

問題

図のように、線分$AB$を直径とする円$O$がある。$\overarc{AB}$上に２点$A,B$とは異なる点$C$をとり、点$C$と2点$A,B$をそれぞれ結ぶ。

また、点$C$を含まない$\overarc{AB}$上に、点$D$を$CB$と$OD$が平行になるようにとり、点$D$と3点$A,B,C$をそれぞれ結ぶ。線分$OB$と線分$CD$の交点を$E$とする。

（１）$\triangle ACD ∽ \triangle DBO$となることを証明しなさい。

（２）$AO=2 cm, CB=3 cm$のとき、線分$BD$の長さを求めなさい。