Study Style
-高校入試スタディスタイル-

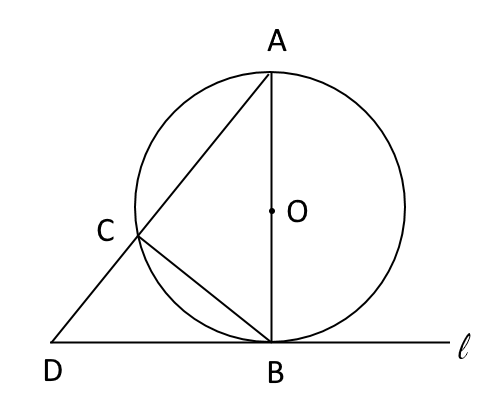
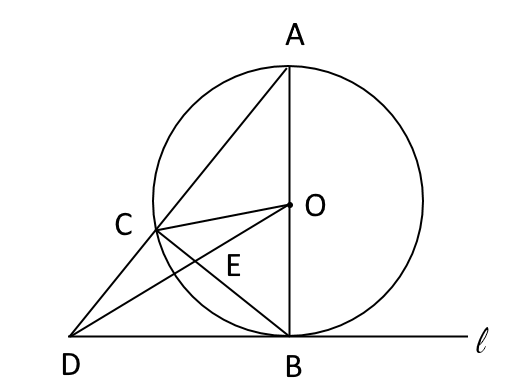
図１

図１のように、点$O$を中心とし、線分$AB$を直径とする円$O$がある。 直線$\ell$は、点$B$を通る円$O$の接線である。 点$C$は、円$O$の周上にあり、点$A,B$と異なる点である。 点$D$は、直線$AC$と直線$\ell$の交点である。

（１）$\triangle ABC $∽$ \triangle ADB$となることを証明しなさい。

（２）略

図２

図２は図１に線分$OC$と線分$OD$をかき加えたもので、 点$E$は線分$BC$と線分$OD$の交点である。

（３）線分$OB$と線分$AD$の長さの比が$OB:AD=3:8$のとき、$\triangle OBE$の 面積は、$\triangle ABD$の面積の何倍か。