Study Style
-高校入試スタディスタイル-

2022年秋田県　１－（１５）

解答

（１）解説参照（２）略（２）$\frac{9}{46}$

解説・解き方の例

（１）

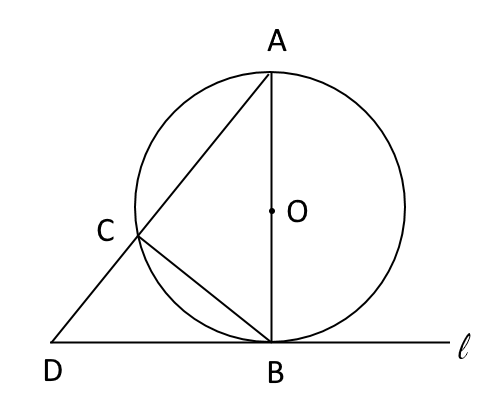
図１

略解：$\angle A$が共通、$\angle ABD = \angle ACB = 90度$より、２角が等しいので$\triangle ABC $∽$ \triangle ADB$である。

（３）この問題を解くには、$CE:EB$か、$OE:ED$のどちらかがわかれば解けるであろうとまず見通しを立てる。そこを目標に解いていく。

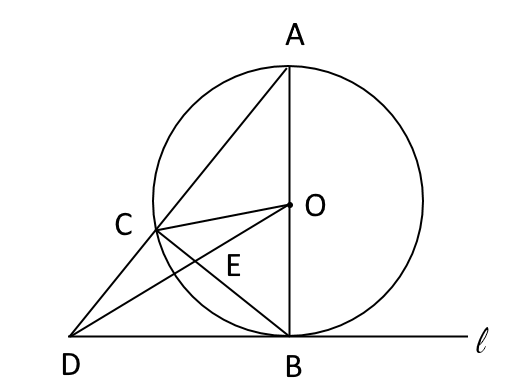
図２

$CE:EB$や、$OE:ED$のように、同じ直線上に並んだ線分の比を求める時に有効な方法の一つが、 その直線に平行な線を利用する（なければ補助線を引く）、ということである。 （問題22でもその方法を利用している）

この場合、$CB$や$OD$に平行な直線がないので、補助線をひくことになる。

$CB$であれば$O$から平行線を引き（図３の$SO$）、 $OD$ならば$C$から平行線を引く（図４の$TC$）。 ここで、どちらのほうがその後に利用しやすいかを考える。

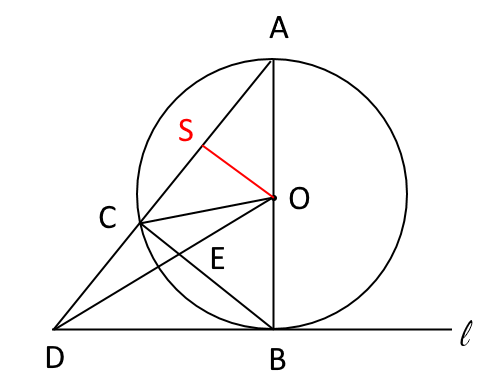
図３

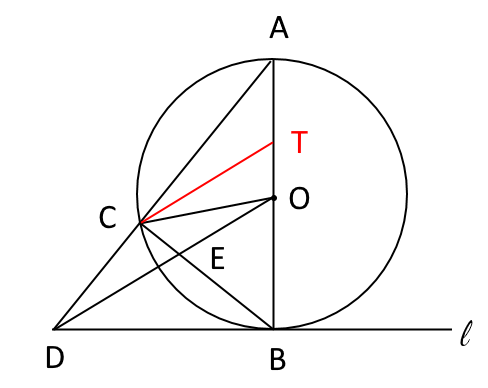
図４

どちらでもよいが、ここでは図３の$SO$を利用する。

まずはじめに、下の図１（再掲）の$AC:CD$は必要になるので、これを先に求めておく。

図１（再掲）

$OB:AD=3:8$より、下の図５のように、$AB:AD=6:8=3:4$である。 そして、$\triangle ADB$で三平方の定理より$DB=2\sqrt{7}$となる。 よって、$AB:AD:DB=3:4:\sqrt{7}$である。

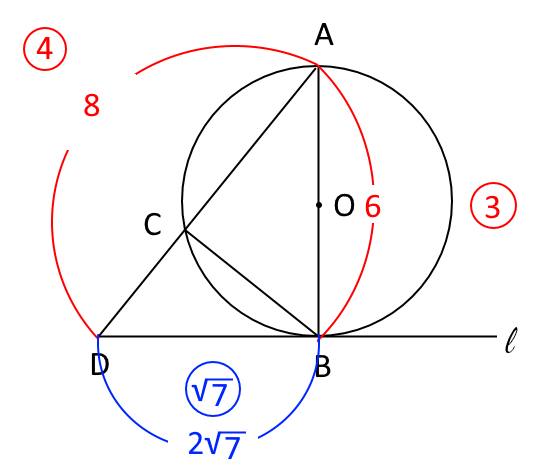
図５

さらに、下の図６のように、$\triangle ADB$∽$\triangle ABC$∽ $\triangle BDC$より（証明略）、対応する各辺の比が図のように $3:4:\sqrt{7}$になる。

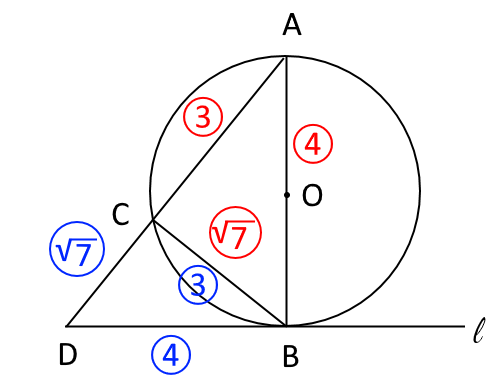
図６

よって、$AC:CB=3:\sqrt{7}$であり、$CB:CD=3:\sqrt{7}$であるので、 $AC:CB:CD=9:3\sqrt{7}:7$となる。つまり、 $AC:CD=9:7$である。

ここで、補助線$SO$を引いたところへ戻ると、図７のように $AO:OB=1:1$,$AC:CD=9:7$のようになっている。

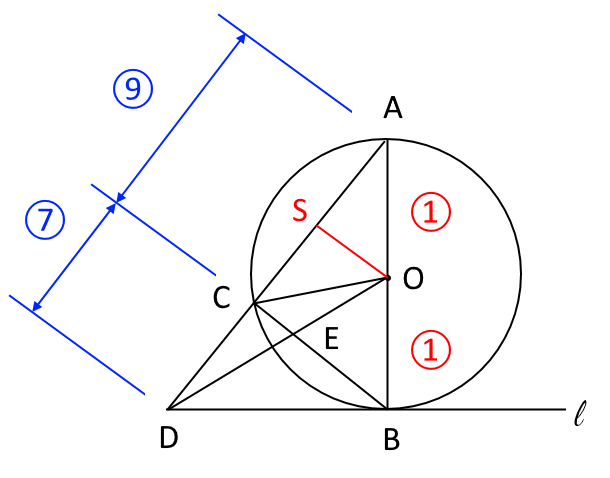
図７

ここで、$SO // CB$より、$AS:SC=AO:OB=1:1$である。

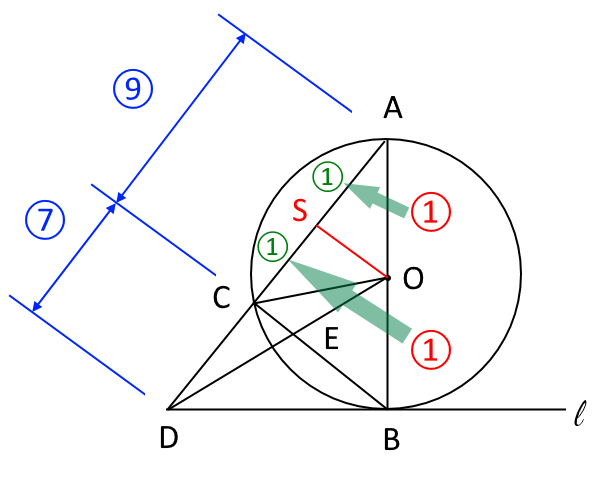
図８

さらに、$AC:CD=9:7$より、$AS:SC=9@9$と考えると、 $AS:SC:CD=9:9:14$となる。

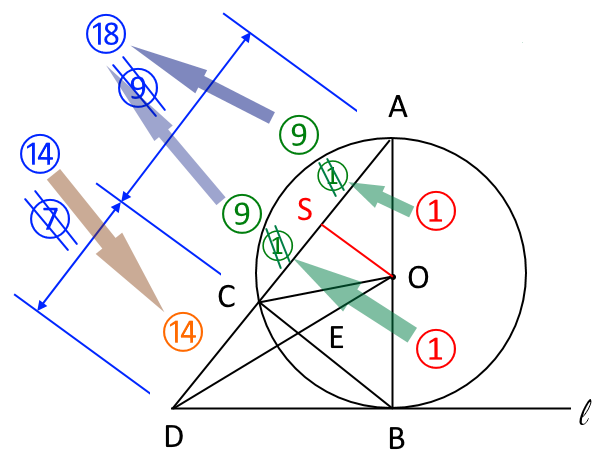
図９

整理すると、次の図１０のような比になる。

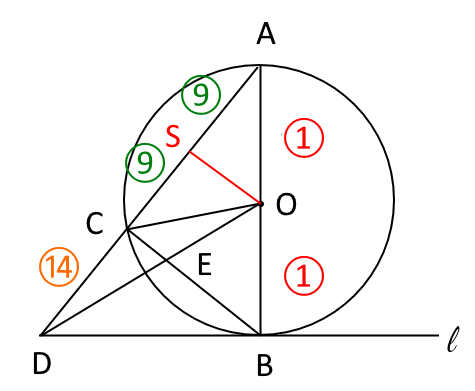
図１０

ここで、$SO=23$とすると、（23は9と14を足したもの） $CE=SO \times \frac{14}{14+9}=14$であり、 $CB=SO \times 2 = 26$より、$EB=CB-CE=46-14=32$となる。

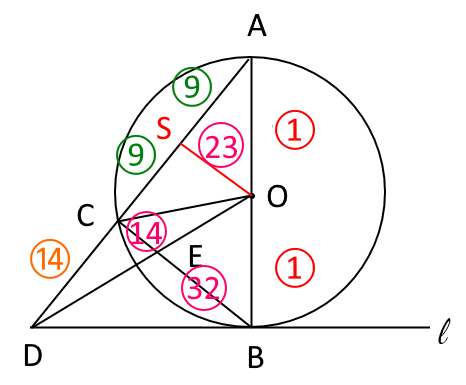
図１１

よって、$CE:EB=14:32=7:16$である。

線分の長さの比がわかったので、ここで、面積の比較に移る。

$\triangle OBE=\frac{16}{23} \times \triangle OBC = \frac{16}{23}\triangle OBC$

$\triangle OBC=\triangle OAC$より、 $\triangle OBC = \frac{1}{2} \triangle ABC$となり、 $\triangle OBE=\frac{8}{23} \triangle ABC$である。

最後に、$\triangle ABC= \frac{9}{16} \triangle ABD$より、 $\triangle OBE = \frac{8}{23} \times \frac{9}{16} \triangle ABD$ $=\frac{9}{46} \triangle ABD$となる。

問題

図１

図１のように、点$O$を中心とし、線分$AB$を直径とする円$O$がある。 直線$\ell$は、点$B$を通る円$O$の接線である。 点$C$は、円$O$の周上にあり、点$A,B$と異なる点である。 点$D$は、直線$AC$と直線$\ell$の交点である。

（１）$\triangle ABC $∽$ \triangle ADB$となることを証明しなさい。

（２）略

図２

図２は図１に線分$OC$と線分$OD$をかき加えたもので、 点$E$は線分$BC$と線分$OD$の交点である。

（３）線分$OB$と線分$AD$の長さの比が$OB:AD=3:8$のとき、$\triangle OBE$の 面積は、$\triangle ABD$の面積の何倍か。