2022年宮城県　４

解答

（１）$2 \sqrt{5} cm$（２）解説参照 （３）$\frac{8 \sqrt{5}}{9} cm^2$ （４）$ED:DG=14:9$

解説・解き方の例

（１）

$\triangle ABC$は$\angle ACB$が直径の円周角で90度であることから、図３のようになっている。

三平方の定理より、$AC^2+BC^2=AB^2$より、$4^2+BC^2=6^2$となり、計算すると$BC=2\sqrt{5} cm$となる。

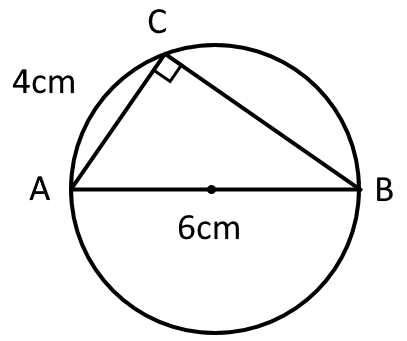
図３

（２）

略解

$\triangle ABC$と$\triangle ADE$で、①$\angle ACB= \angle AED=90度$、 ②$\angle A$は共通、より、$\triangle ABC$ ∽ $\triangle ADE$(二角相当）となる。

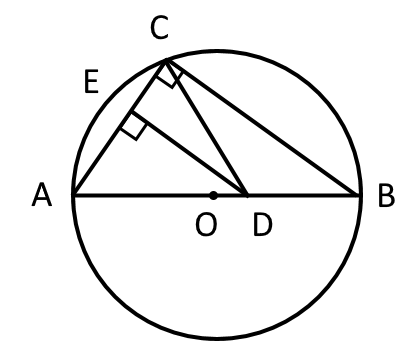
図３

（３）

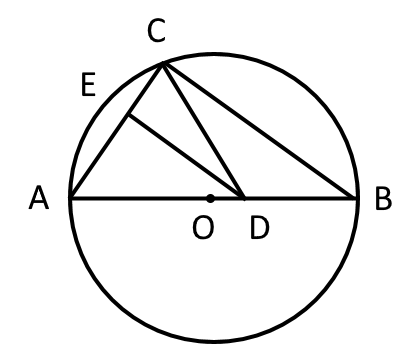
図１（再掲）

図１において、$\triangle ABC$ ∽ $\triangle ADE$より、$AE:EC=AD:DB=4cm:2cm=2:1$なので $EC=AC \times \frac{1}{3} = \frac{4}{3} cm$である。

同様に、$DE:BC=AB:AD=6 cm : 4cm=3:2$より、(1)の結果を使って、 $ED = 2\sqrt{5} \times \frac{2}{3} = \frac{4\sqrt{5}}{3} cm$となる。

よって、$\triangle CED$の面積$S$は$\angle DEC$が90度であることから、 $S=EC \times DE \div 2 = \frac{4}{3} \times \frac{4\sqrt{5}}{3} \div 2 = \frac{8 \sqrt{5}}{9} cm^2$となる。

（４）

この問題はなかなか難しい。間違えやすいのが、$AC$と$FB$が平行であると思いこんで 問いてしまうことである。

解くための取っ掛かりとしては、次のように考えるとよいかもしれない。

1. $ED$は長さがわかるが、$DG$は$DG$と$FB$が垂直でもなく三平方の定理などを使えず、長さを求めにくい。
2. そこで、$DG$の長さや比を求めるためには、$EG // CB$であることから、 $\triangle FDG$と$\triangle FCB$の相似を利用して$CB$から$DG$を求めるのがよさそうである。
3. $DG$を求めるには、$CD:DF$や$BG:GF$などがわかる必要がある。

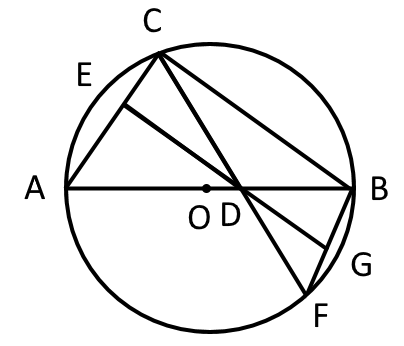
図２（再掲）

そこで、ここでは$CD:DF$を求めることにする。

$\triangle CED$は直角三角形なので、$CD^2=CE^2+DE^2$より、 $ED=\frac{4\sqrt{5}}{3}$を使って、 $CD^2=\left(\frac{4}{3}\right)^2 +\left(\frac{4\sqrt{5}}{3}\right)^2=\frac{16}{9}+\frac{80}{9}$ $CD^2=\frac{96}{9}$より、$CD=\frac{4\sqrt{6}}{3}$となる。

次に、$\triangle DAC$と$\triangle DFB$は、下の図の●と★が円周角で等しいことから、 $\triangle DAC$ ∽ $\triangle DFB$となる。

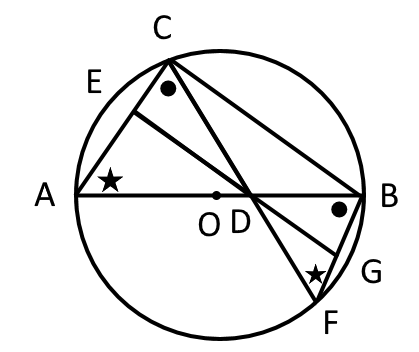
図４

よって、対応する辺の比が等しいので、$AD:DC=FD:DB=4 : \frac{4 \sqrt{6}}{3} = FD : 2$より $FD = \sqrt{6}$となる。（ここで方べきの定理をつかってもよい）

よって、$CD:DF=\frac{4\sqrt{6}}{3}:\sqrt{6}=4:3$より、 $DG=\frac{3}{4+3}\times CB=\frac{3}{7}CB$となる。

また、$ED=\frac{2}{3}CB$なので、 $ED:DG = \frac{2}{3}CB:\frac{3}{7}CB=\frac{2}{3}:\frac{3}{7}=14:9$となる。

問題

図１

図１のように、長さが$6 cm$の線分$AB$を直径とする円$O$がある。 図１のように、円$O$の周上に$AC = 4 cm$となる点$C$をとり、 点$B$と点$C$を結ぶ。また、線分$AB$上に$AC = AD$となる点$D$をとり、点$C$と点$D$を結ぶ。 さらに、点$D$から線分$AC$に垂線をひき、線分$AC$との交点を$E$とする。

（１）線分$BC$の長さを求めなさい。

（２）$\triangle ABC$ ∽ $\triangle ADE$であることを証明しなさい。

（３）$\triangle CED$の面積を求めなさい。

（４）図２は図１において、線分$CD$を$D$の方に延長した直線と円$O$との交点を$F$とし、 点$F$と点$B$を結んだものである。また、線分$ED$を$D$の方に延長した直線と線分$BF$との交点を$G$とする。 線分$ED$と線分$DG$の長さの比を求めなさい。