2022年青森県　３－１

解答

（１）$6 \sqrt{2} cm$（２）$10 cm$

解説・解き方の例

（１）

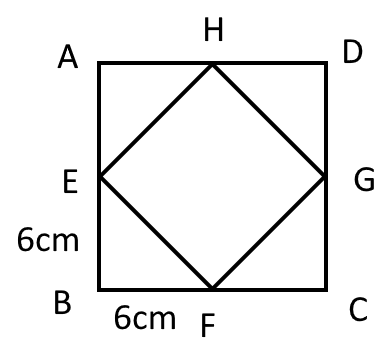
図2

底面は図２のようになっている。

$\triangle BEF$は45度の直角三角形なので、$EF=6\sqrt{2} cm$となる。

（２）

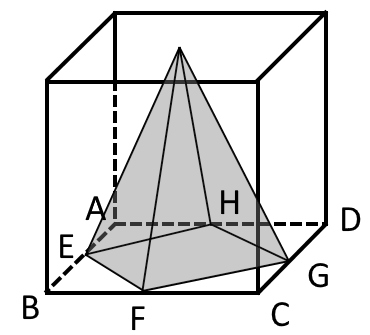
図3

★解法１★　実際の体積を求める。

立方体の体積は $V1 = 12 \times 12 \times 12 = 1728 cm^3$

正四角すいの体積は $V2 = (6\sqrt{2})^2 \times 12 \times \frac{1}{3} = 288 cm^3$

水の容積は$V1 - V2 = 1728 - 288 = 1440 cm^3$

よって、水の深さは底面積で割って、$1440 \div (12 \times 12) = 10 cm$

★解法２★　体積の比を求める。

（１）の図２からわかるように、正四角すいの底面積は、立方体の底面$ABCD$の半分である。

正四角すいと立方体は高さは同じであるが、正四角すいの体積は 高さに$\frac{1}{3}$を掛けることから、正四角すいの体積は立方体の体積の $\frac{1}{2} \times \frac{1}{3} = \frac{1}{6}$倍になる。 ($\frac{1}{2}$は底面積の割合、$\frac{1}{3}$は高さに$\frac{1}{3}$を掛けるということから)

このことから、正四角すいを水中から除くと、$\frac{1}{6}$だけ水面がさがることになる。 もとの立方体の高さが$12 cm$なので、水面の高さは$10 cm$である。

問題

図１

図１のように、１辺の長さが$12 cm$である立方体の容器が水平に固定されている。 その容器の中には、面$EFGH$を底面とし、高さが$12 cm$の正四角すいが入っており、 点$E,F,G,H$は容器の底面$ABCD$の各辺の中点にある。

（１）辺$EF$の長さを求めなさい。

（２）容器の中にいっぱいになるまで水を入れ、 その後、容器の外に水をこぼすことなく正四角すいを取り出したとする。 このとき、容器の中にある水の底面$ABCD$から水面までの高さを求めなさい。