2021年山形県－４

解答

（１）$80°$、（２）解説参照、（３）$\frac{\sqrt{7}}{3} cm^2$

解説・解き方の例

（１）

$\angle BGE$が40°（次の図の赤い丸）である。

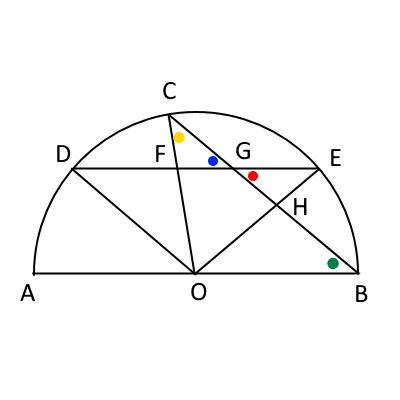
すると、青い丸は、赤い丸の対頂角で40°。

緑の丸は、$DE//AB$より、赤い丸と錯角で40°

黄色い丸は、$\triangle OBC$が二等辺三角形($OB=OC=半径$)なので、 緑の丸と同じなのでやはり40°。

よって、緑の丸＋黄色い丸=$\angle AOC$なので、80° となる。

（２）略解

証明するのは、次の図の赤と青の三角形の合同である。

$\angle COH=\angle EOF$（共通）および、$OC=OE$（円の半径）はすぐにわかるので、 あとひとつの合同の条件を見つければよい。

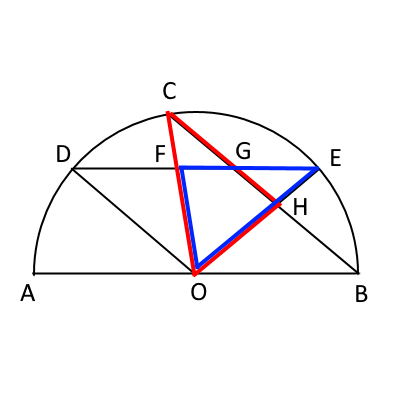
そこで、$\angle OCH$と$\angle OEF$が等しいことを示す。

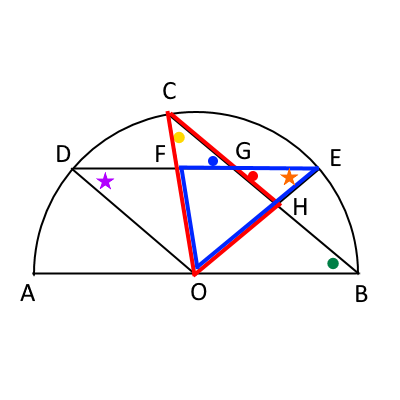
次の図で、前問で赤、青、緑、黄色の丸が角度が同じであった。 さらに、問題の条件（設定）より、$ODGB$は平行四辺形であるから、 緑の丸と紫の星は同じ大きさである。（平行四辺形の対角）

さらに、紫の星とオレンジの星は同じ大きさである。（$\triangle ODE$は二等辺三角形なので） よって、黄色の丸とオレンジの星は同じ大きさである。 したがって、赤と青の三角形は合同である。

（３）

方針

最初にわかっていることを整理すると、

1. $\triangle CFG$は二等辺三角形である。
2. $\triangle CFG$と$\triangle COB$は相似である。

である。したがって、$CF,FG$や$CGの長さが分かれば面積がわかるであろうと目星をつける。

問題では$DE$の長さが与えられていることから、$FG$の長さを求めることを目標として解いてみる。

$FG$を求める。

方針：$FG=x$とおいて式をたて、$x$を求める。

まず、前問でもあったとおり、等しい角度がたくさんあり、相似の二等辺三角形がたくさんあることを確認する。 $\triangle CFG,\triangle EHG,\triangle FDO,\triangle ODE,\triangle OBC$などはみんな二等辺三角形であり、相似である。

四角形$ODEB$が平行四辺形であることに注意すると、 $DF+FG=DG=OB=4 cm$である。よって、$GE=DE-DG=2 cm$となる。

$GE=GC$であり、$FG:GC=OD:DE=4:6=2:3$である。よって、$GE=\frac{3}{2}x$である。

よって、$\frac{3}{2}x=2 cm$より、$x=\frac{4}{3} cm$となる。

$\triangle CFG$の面積

$\triangle CFG$は次のようになっている。

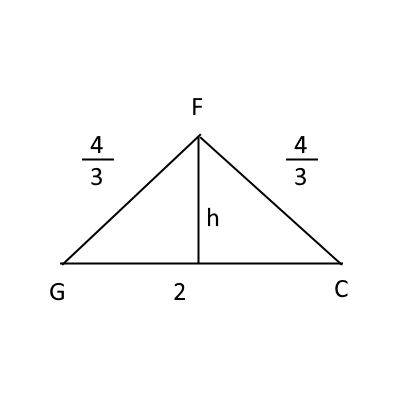
三角形の高さ$h$は、三平方の定理より、 $$h^2+1^2=\left(\frac{4}{3}\right)^2$$ より、 $$h^2=\frac{7}{9}$$ よって、 $$h=\frac{\sqrt{7}}{3}$$ となる。

よって、面積は、 $$2 \times \frac{\sqrt{7}}{3}\times \frac{1}{2}=\frac{\sqrt{7}}{3} cm^2$$ となる。

問題

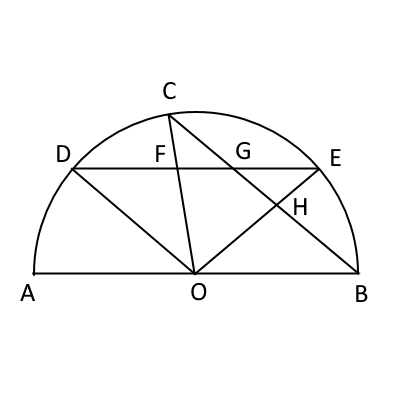
図のように、点$O$を中心とし、線分$AB$を直径とする半円$O$がある。 点$A$とは異なる点$C$を、弧$AB$上に、$\angle AOC$の大きさが$90°$より小さくなるようにとる。

また、点$D$を、弧$AC$上に、$OD // BC$となるようにとる。 点$D$を通り、線分$AB$に平行な直線と半円$O$との交点のうち、点$D$とは異なる点を$E$とする。 線分$DE$と線分$OC,BC$との交点をそれぞれ$F,G$とし、線分$OE$と線分$BC$との交点を$H$とする。

（１）$\angle BGE=40°$であるとき、$\angle AOC$の大きさを求めなさい。

（２）$\triangle OCH \equiv \triangle OEF$であることを証明しなさい。

（３）$AB=8 cm, DE=6 cm$であるとき、$\triangle CFG$の面積を求めなさい。