Study Style
-高校入試スタディスタイル-

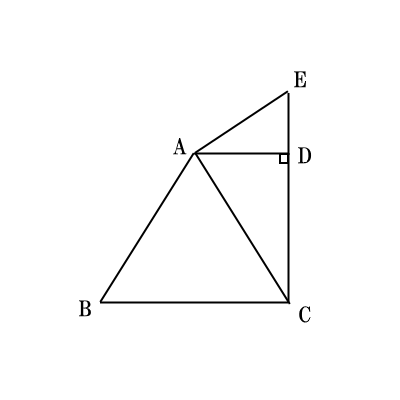
図のような$AD$と$BC$が平行, $BC=2AD,$ $AD \lt CD $ $,\angle ADC=90°$の台形$ABCD$があります。 線分$CD$を$D$の方に延長した直線上に$\angle CAE=90°$となる点$E$をとります。

（１）$\triangle ACD$∽$\triangle ECA$であることを証明しなさい。

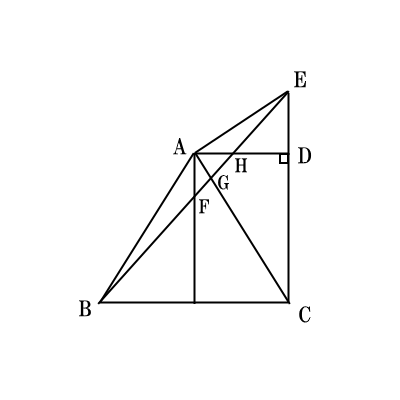
次の図は点$B$と点$E$を結んだものです。また、点$A$から線分$BC$に垂線をひき、線分$BE$ との交点を$F$とします。 さらに、線分$BE$と線分$AC,AD$との交点をそれぞれ$G,H$とします。 $AD=2 cm,CD=3 cm$のとき、次の問に答えなさい。

（２）線分$DE$の長さを求めなさい。

（３）$\triangle EHD$の面積を求めなさい。

（４）線分$FH$と線分$GH$の長さの比を求めなさい。