2021年宮城県－４

解答

（１）解説参照、（２）$\frac{4}{3} cm$、（３）$\frac{32}{39} cm^2$、（４）$31:18$

解説・解き方の例

（１）略解

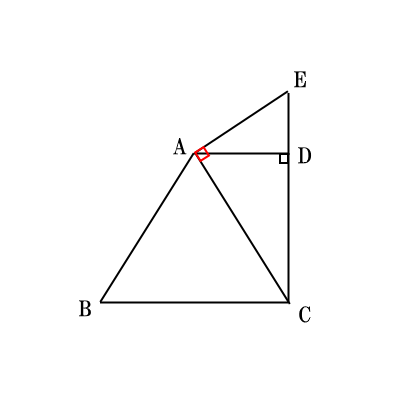
図の赤い角度が直角なので、これを利用して証明すればよい。

$\angle CDA=\angle CAE=90°$,$\angle ACD$は共通、という2点から相似を証明する。（証明略）

（２）

(1)で$\triangle ACD$∽$\triangle　ECA$を証明したので、これを利用する。

まず、三平方の定理より$AC^2=AD^2+CD^2$となるので、$AC^2=2^2+3^2=13$

よって、$AC=\sqrt{13}$である。

相似の三角形の対応する辺の比より、$CD:AC=AC:CE$より、$CE=x$として、 $$3:\sqrt{13}=\sqrt{13}:x\\ x=\frac{13}{3}$$ よって、$CD=3$より、 $$DE=CE-CD=\frac{13}{3}-3=\frac{4}{3} cm$$ となる。

（３）

相似である$\triangle EHD$と$\triangle EBC$に注目する。

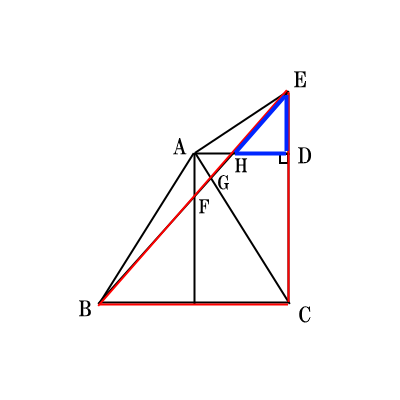
相似比は、$\triangle EHD:\triangle EBC=ED:EC=\frac{4}{3}:\frac{13}{3}=4:13$

よって、面積比は2乗なので、$4^2:13^2=16:169$である。

$\triangle EBC$の面積は$BC=4,EC=\frac{13}{3}$より、 $$4 \times \frac{13}{3} \times \frac{1}{2}=\frac{26}{3}$$ なので、面積比を使って、 $$\triangle EHD = \frac{26}{3} \times \frac{16}{169} = \frac{32}{39} cm^2$$ となる。

（４）

＄FH$と$GH$を比を求めるにはいくつか方法がある。直接長さを求めることも不可能ではないが、あまり良い方法ではないので、ここでは相似比を利用した方法を紹介する。

使う相似は次の2つの相似である。

・相似１（赤と青の三角形）

①$FH:HE=AF:ED$を使う。

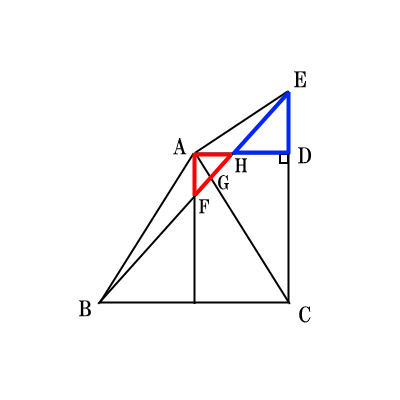
・相似２（オレンジと緑の三角形）

②$FG:GE=AF:CE$を使う。

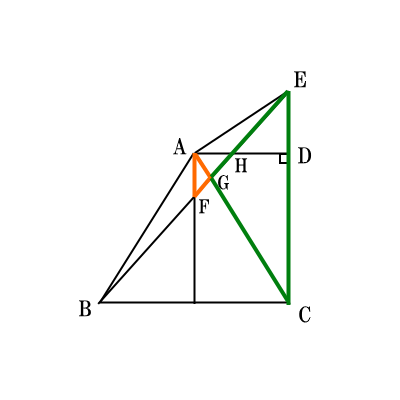
①、②のどちらの場合も$AF$の長さを用いるので、まずは$AF$の長さを求める。

$AF$の長さ

$AF$を求めるには、次の図の相似を用いる。$A$から$BC$への垂線の足を$I$とすると、 $BI:BC=1:2$なので、$IF:CE=1:2$より、$$IF=CE\times \frac{1}{2}=\frac{13}{3}\times \frac{1}{2}=\frac{13}{6}$$である。 $AI=3$より、$$AF=3-\frac{13}{6}=\frac{5}{6} cm$$ となる。

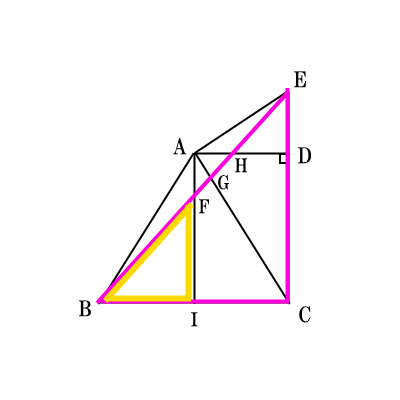
$FH$について

先にあげた、相似１を使って、$FH$の$FE$に対する割合を求めてみる。

$FH:HE=AF:ED$ $=\frac{5}{6}:\frac{4}{3}=5:8$ より、$FH=\frac{5}{5+8}\times FE=\frac{5}{13}\cdot FE$となる。

$FG$

相似２を使って、$FG$の$FE$に対する割合を求めてみる。

$FG:GE=AF:CE$ $=\frac{5}{6}:\frac{13}{3}=5:26$ より、$FG=\frac{5}{5+26}\times FE=\frac{5}{31}\cdot FE$となる。

$FH:GH$

よって、$$FH:GH=\frac{5}{13}\cdot FE:\left(\frac{5}{13}-\frac{5}{31}\right)\cdot FE\\ \frac{5}{13}:\left(\frac{5}{13}-\frac{5}{31}\right)=\\ \frac{1}{13}:\left(\frac{1}{13}-\frac{1}{31}\right)=\\ 31:(31-13)=31:18 $$ となる。

問題

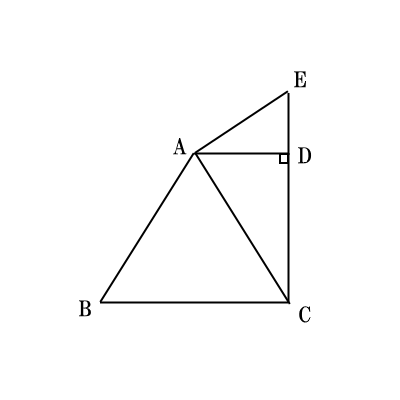
図のような$AD$と$BC$が平行, $BC=2AD,$ $AD \lt CD $ $,\angle ADC=90°$の台形$ABCD$があります。 線分$CD$を$D$の方に延長した直線上に$\angle CAE=90°$となる点$E$をとります。

（１）$\triangle ACD$∽$\triangle ECA$であることを証明しなさい。

次の図は点$B$と点$E$を結んだものです。また、点$A$から線分$BC$に垂線をひき、線分$BE$ との交点を$F$とします。 さらに、線分$BE$と線分$AC,AD$との交点をそれぞれ$G,H$とします。 $AD=2 cm,CD=3 cm$のとき、次の問に答えなさい。

（２）線分$DE$の長さを求めなさい。

（３）$\triangle EHD$の面積を求めなさい。

（４）線分$FH$と線分$GH$の長さの比を求めなさい。