2021年秋田県－３

解答

（１）解説参照（２）$\frac{11}{2}$倍

解説・解き方の例

（１）略解

$\triangle BCE$と$\triangle DCF$の相似を証明すればよい。

（２）

この問題はよくできた、なかなかおもしろい設定になっている。

$ED:DC=1:3$という普通の問題の設定に見えるが、これは、正方形$ABCD$と正方形$ECFG$の辺の長さの比（相似比）が3:4であること、 つまり、（１）で出てきた$\triangle BCE$で、$BC:CE=3:4$となることから、$\triangle BCE$や$\triangle DCF$、さらには$\triangle HDE$が $3:4:5$の比の直角三角形になっているということに気づくかどうかということなのである。

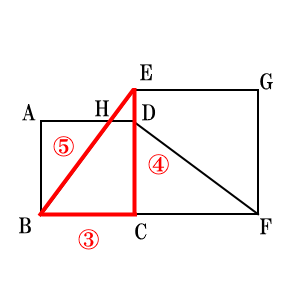
これがわかると後は簡単であろう。まず、 小さい三角形$\triangle EHD$の$HD=3$と仮に長さを設定する。

すると、$DE=4,EH=5$となるので、$\triangle EHD$の周の長さは$3+4+5=12$となる。

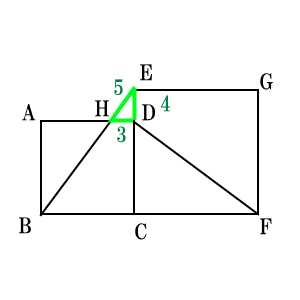
次に、四角形$HBFD$の周の長さは次の図のように、合計$66$になる。

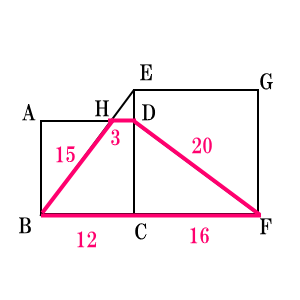
よって、四角形$HBFD$の周の長さは$\triangle EHD$の周の長さの $$\frac{66}{12}=\frac{11}{2}倍$$ となる。

問題

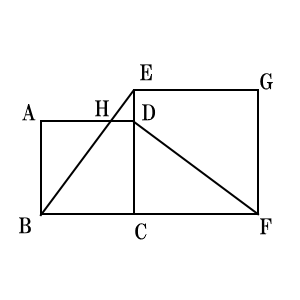
図のように、正方形$ABCD$と正方形$ECFG$があり、３点$E,D,C$は同一直線上にある。 辺$AD$と線分$BE$の交点を$H$とするとき次の問に答えなさい。

（１）$BE=DF$となることを証明しなさい。

（２）線分$ED$と線分$DC$の長さの比が、$ED:DC=1:3$のとき、四角形$HBFD$の周の長さは$\triangle EHD$の周の長さの何倍か。