Study Style
-高校入試スタディスタイル-

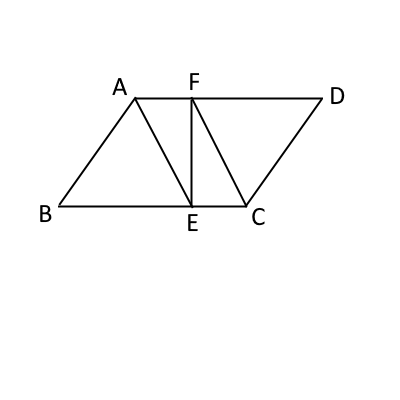
図のように、平行四辺形$ABCD$ があり、辺$BC$上に点$E$を、$BE:EC=5:2$となるようにとる。 また、辺$AD$上に点$F$を、$\angle AEF=\angle CFE$となるようにとる。

（１）四角形$AECF$は平行四辺形であることを証明せよ。

（２）線分$AC$と線分$EF$との交点を$G$、直線$AE$と直線$CD$との交点を$H$とするとき、 四角形$CGEH$と平行四辺形$ABCD$の面積の比をもっとも簡単な整数の比で表せ。