2021年京都府－４

解答

（１）解説参照
（２）四角形$CGEH$:平行四辺形$ABCD$=$9:70$

解説・解き方の例

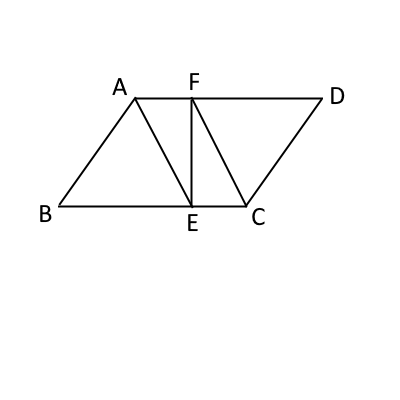
（１）略解

下図で、$AF$と$EC$は平行、また、$\angle AEF=\angle CFE$より、錯角が等しいので、$AE$と$FC$が平行、という２点を言えばよい。

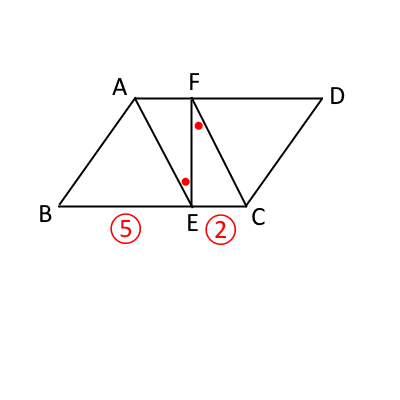
（２）

点$G$、点$H$および四角形$CGEH$は次の図のようになる。

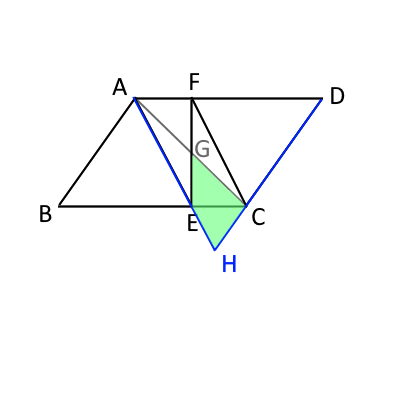
四角形$CGEH$は長方形や正方形など、簡単に求められる形をしていないので、面積や面積比の求め方としては、 多くの場合、①求めやすい三角形・四角形を組合あわせ足し合わせる、または、②求めやすい形から求めやすい形を引いて求める、の２通りである。

この場合も、①$\triangle GEC + \triangle CEH$とするか、②$\triangle AHC-\triangle AEG$とするか、の２通りが考えられるが、 ここでは、②$\triangle AHC-\triangle AEG$の方を使って解いてみる。

重要な比

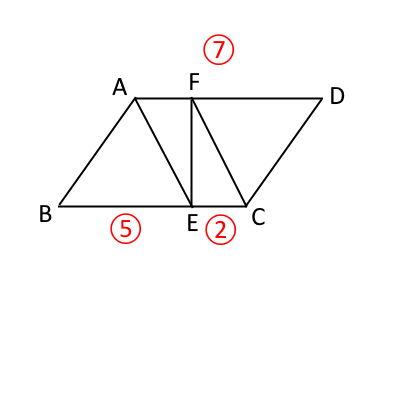
ここで、この問題で多く使う比を確認しておく。 それは、$BE:EC=5:2$で、すなわち、$AD:BE:EC=7:5:2$という比。

重要な相似

比に関連して、重要な相似を確認しておく。それは、下の図の緑・赤・青の３つの三角形の相似である。

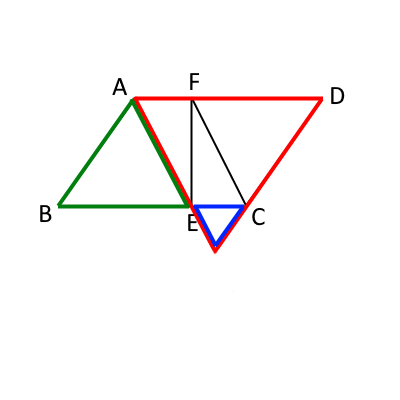
先程の辺の長さの比を当てはめると、次の図のようになっており、相似比：$緑:赤:青=5:7:2$ となり、 したがって、面積比：$緑:赤:青=25:49:4$になる。

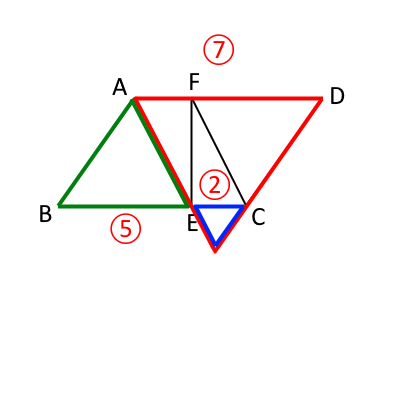
すると、下のオレンジの台形との面積比は、$緑:オレンジ:青=25:(49-4):4=25:45:4$になる。

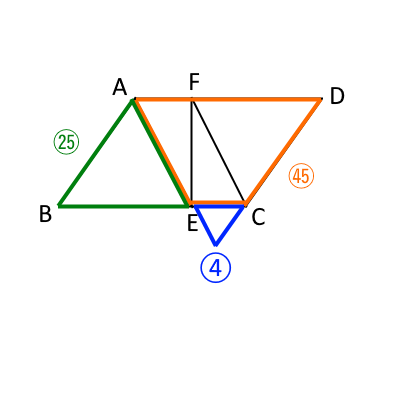
面積比の整理

ここで、今求めた面積比を使うと、元の平行四辺形$ABCD$と、次図の紫の三角形の面積比は$25+45:45+4=70:49=10:7$になることがわかる。

つまり、紫の三角形は元の平行四辺形$ABCD$の$\frac{7}{10}$倍である。

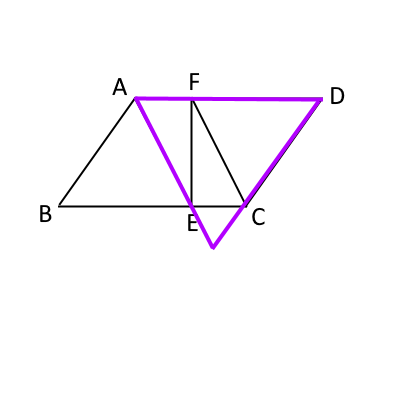
さらに、次のように三角形に分ける。

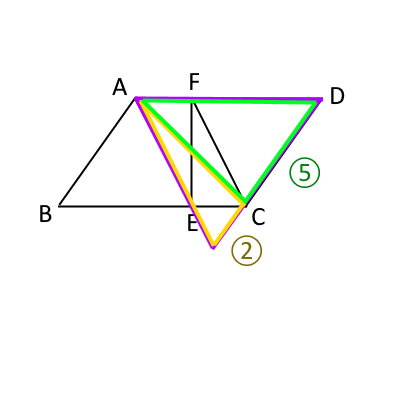
黄色い三角形と緑の三角形の面積比は$黄色:緑=2:5$なので、黄色は紫の三角形の$\frac{2}{7}$倍である。

よって、黄色い三角形は元の平行四辺形$ABCD$の$\frac{7}{10}\times \frac{2}{7}=\frac{1}{5}$倍である。

四角形$CGEH$

さて、元の四角形$CGEH$の図を見てみると、次の図のようになっている。

図で、四角形$AECF$は平行四辺形なので、$AG:GC=1:1$。相似比から$AE:EH=5:2$である。

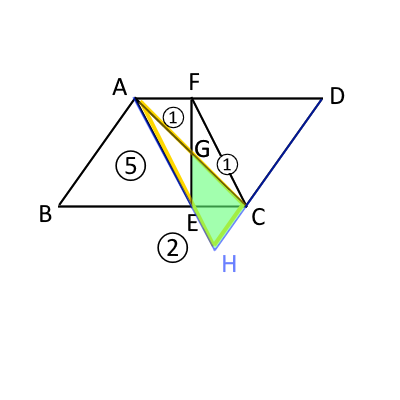
$\triangle AEB$の面積が$\triangle AHC$の面積の何倍になっているかは次の「豆知識」を使う。

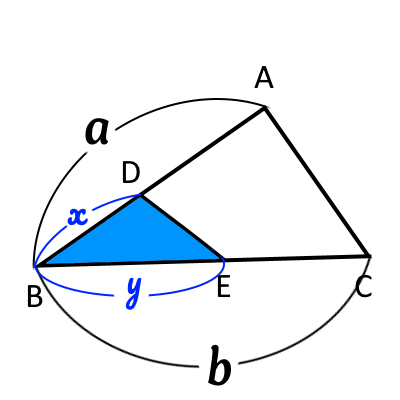
「豆知識」を使うと、$\triangle AHC:\triangle AEG=7\times 2:5\times 1=14:5$となる。

よって、$\triangle AEG=\triangle AHC \times \frac{5}{14}$である。

よって、四角形$CGEH=\triangle AHC\times (1-\frac{5}{14})=\triangle AHC \times \frac{9}{14}$となる。

前の方の図で、黄色い三角形（$\triangle AHC$）は元の平行四辺形$ABCD$の$\frac{1}{5}$倍なので、 四角形$CGEH=\triangle AHC \times \frac{9}{14}$ $=平行四辺形ABCD \times \frac{9}{14} \times \frac{1}{5}$ $=平行四辺形ABCD \times \frac{9}{70}$ となる。

よって、$四角形CGEH :平行四辺形ABCD=9:70$となる。

問題

図のように、平行四辺形$ABCD$ があり、辺$BC$上に点$E$を、$BE:EC=5:2$となるようにとる。 また、辺$AD$上に点$F$を、$\angle AEF=\angle CFE$となるようにとる。

（１）四角形$AECF$は平行四辺形であることを証明せよ。

（２）線分$AC$と線分$EF$との交点を$G$、直線$AE$と直線$CD$との交点を$H$とするとき、 四角形$CGEH$と平行四辺形$ABCD$の面積の比をもっとも簡単な整数の比で表せ。