2021年京都府－５

解答

（１）半径$6cm$、体積$144\pi cm^3$
（２）$AD:EF=6:5$（３）$256\pi cm^3$

解説・解き方の例

（１）

半径を$r$とすると、$2 \pi r = 12 \pi$より、$r=6 cm$

体積は、$$\frac{4}{3} \pi r^3 \times \frac{1}{2}\\ =\frac{4}{3} \pi 6^3 \times \frac{1}{2}=144 \pi cm^3$$

（２）

台形を回転させた図形（円すい台）の基本

今回のような台形を回転させた図形を円すい台というが、 この立体図形の基本は次の図のように断面図の比率をつかむことが重要。

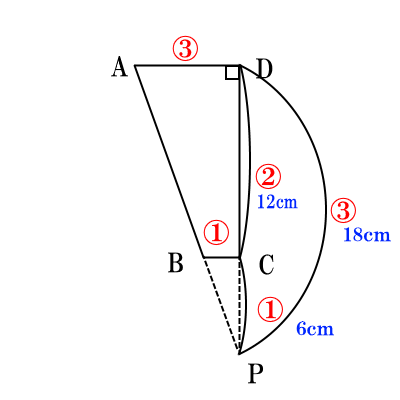
$AD:BC=3.1, CD=12 cm$ と与えられているので、 このように$AB$と$DC$を延長した交点を$P$とすると、三角形の相似より、 $DP:CP=AD:BC=3:1$となるので、$CP=6cm,DP=18cm$というのがわかる。

水面$EF$による相似三角形

ここで、水面の$EF$を描いてみると、次のようになっている。

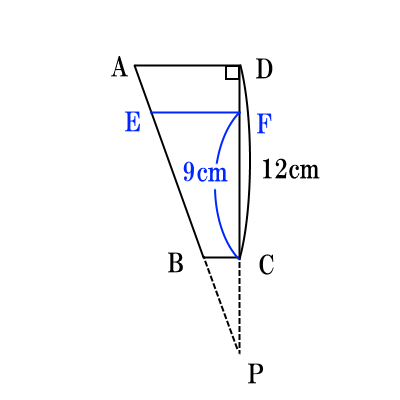
ここで、$\triangle ADP$と$\triangle EFP$という二つの相似三角形に注目すると、 $CP=6cm$ということから、$CF=15cm, PD=18cm$ということがわかる。 よって、相似の三角形の対応する辺の比より、 $$AD:EF=DP:FP=18:15=6:5$$ となる。

（３）

線分比

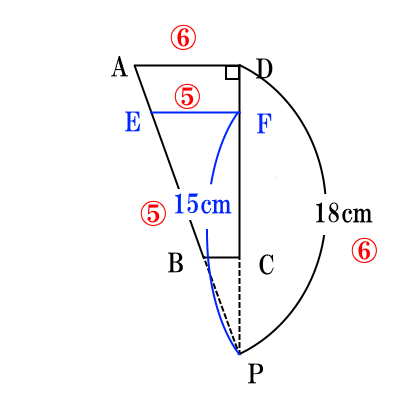
まず、$AD:EF:BC$の線分比を求める。次の図のように、$AD:BC=3:1$,$AD:EF=6:5$なので、 まとめると、$AD:EF:BC=6:5:2$になる。

相似比から体積比

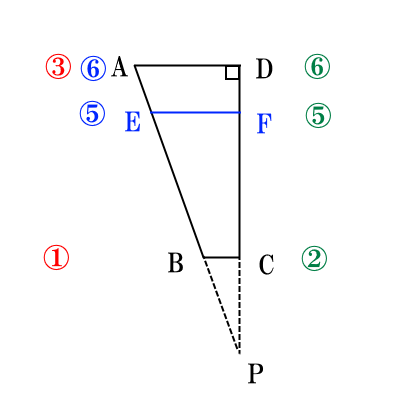
次の図で、まず$\triangle ADP,\triangle EFP,\triangle BCP$の相似比は、線分比と同じなので、$\triangle ADP:\triangle EFP:\triangle BCP=6:5:2$になる。

体積比は相似比の3乗なので、$\triangle ADP:\triangle EFP:\triangle BCP=6^3:5^3:2^3$ $=216:125:8$となる。

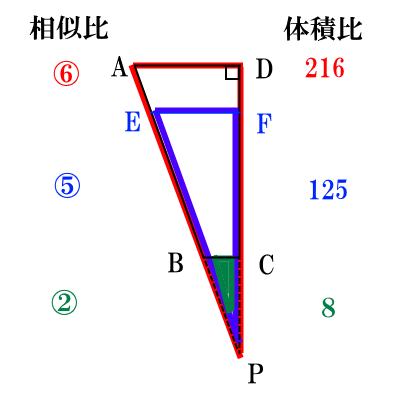
ここで、$四角形ABCD$を回転させた部分が容器Yの容量、$四角形EBCF$を回転させた部分が容器Xの容量（水の量）である。 これをさきほどの体積比を使って表すと、容器Yの容量が$216-8=208$、容器Xの容量が$125-8=117$となる。

容器Xの容量は$144 \pi cm^3$なので、容器Yの容量を$x$とおくと、 $$x:144 \pi=208:117$$となる。 $208$と$117$は$13$の倍数であることに注意すると、 $$x:144 \pi=208:117=16:9$$ となるので、 $$9x=144 \times 16\\ x=144 \times 16 \div 9 =256$$ より、容器Yの容量は$256 cm^3$である。

※208と117が13の倍数というのは気が付きにくいので要注意！

問題

点$O$を中心とする球を、点$O$を通る平面で切ってできる半球の形をした容器Xがあり、 I図のように、切り口を水平に保って満水にしてある。 この切り口を円$O$とすると、円$O$の周の長さは$12\pi$であった。

また、II図のように、$AD$と$BC$が平行の台形$ABCD$があり、$AD:BC=3:1,CD=12 cm,$ $\angle ADC=90°$である。台形$ABCD$を、直線$CD$を回転の軸として１回転させてできる 立体の形をした容器Yがあり、空の容器Yを、$BC$を半径とする円$C$が底になるように水平な台の上に置く。

III図のように、容器Yに、容器Xに入っている水を残らず注ぐと、容器の底から水面までの高さは$9 cm$になった。 水面と線分$AB$、線分$CD$との交点をそれぞれ$E,F$とする。

（１）円$O$の半径を求めよ。また、I図において、容器Xに入っている水の体積を求めよ。

（２）$AD:EF$をもっとも簡単な整数の比で表わせ。

（３）容器Yの容積を求めよ。